Основные операции с объемами и содержаниями понятий составляют часть так называемой теории множеств. К операциям с объемами понятий относятся пересечение, объединение, дополнение и вычитание.
Пересечение. С использованием языка логики предикатов операция пересечения запишется следующим образом:
где W – оператор образования множества из понятия (оператор выделения объема понятия из самого понятия). W указывает на то, что речь идет именно об объемах понятий; Ç – знак пересечения.
Если мы ищем пересечение, то для разных видов совместимых и несовместимых понятий результаты пересечений их объемов будут разными (рис. 5).
Рис. 5. Пересечение: а – тождественные понятия; б – перекрещивающиеся понятия; в – подчиненное и подчиняющее понятия; г – несовместимые (соподчиненные) понятия
Объединение. Операция объединения запишется так:
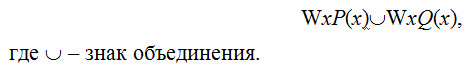
Объединение объемов понятий также может иметь различные варианты (рис. 6).
Дополнение. Дополнением объема понятия хР(х) до универсума области возможных значений переменной х называется множество тех элементов этого универсума, которые не принадлежат понятию хР(х) (рис. 7). Записывается дополнение следующим образом:
WxP(x)
Вычитание. Формула вычитания имеет следующий вид:
WxP(x)\WxQ(x),
где \ – знак вычитания объема одного понятия из объема другого.
Вычитание объемов понятий имеет разные варианты (рис. 8).
Рис. 8. Вычитание: а – тождественные понятия; б – перекрещивающиеся понятия; в, г – подчиненное и подчиняющее понятия; д – несовместимые (соподчиненные) понятия
