Логика - доступно для всех

Построение логических высказывании предполагает:

1. Выделим некоторые простые предложения (A,B,C,…), то есть высказывания, относительно которых можно сказать: истина или ложь.
2. Каждое рассматриваемое предложение (высказывание) состоит из простых с помощью сентециональных связок.

Пусть дано непустое множество отдельных предложений; расширим это множество, присоединив к нему как раз те предложения, которые можно образовать, используя многократно и всевозможными способами различные сентенциональные связки. В таком случае это расширенное множество будет обладать следующим свойством:

Если A и B – элементы этого множества, то его элементами  будут и .

Будем называть элементы этого расширенного множества формулами. Элементы первоначального множества называют простыми (или элементарными) формулами, а остальные – составными формулами.

О простых формулах, входящих в составную, говорят что они содержатся  в ней, и называют их ее простыми компонентами.

Если простыми компонентами формулы А служат , то определение истинностного значения формулы А при истинностными значениям компонентов  можно представить в виде таблицы истинности. Такая таблица состоит из  строк, каждая из которых изображает одно из возможных распределений T и F, приписываемых компонентам .

Истинностная функция есть функция, определенная на  со значениями в V, где  и . Иными словами, истинностная функция есть функция от n аргументов, причем каждый аргумент может принимать значение T или F и сама функция имеет значение T или F. Мы будем обозначать истинностные функции символами:

Обозначим другим способом:

Данное обозначение указывает на функцию, полученную из истинностных функций с аргументами и  с аргументами. Мы будем говорить об этой функции, если она получена подстановкой функции g вместо i-ой переменной в .

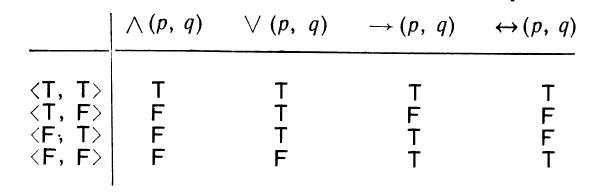
Существует различных истинностных функций от  переменных. Из четырех, соответствующих , ту, которая имеет значение F при T и T при F, мы будем обозначать . Из шестнадцати функций истинности, соответствующих , мы выделим четыре. Их определения и обозначения даны в следующей таблице:

Покори английский в игровой форме! Основные преимущества:

• Занимайся с любого девайса
• Тренируйся с азартом
• Выбирай интересные материалы
• Проходи увлекательные языковые курсы
• Учись со львом играючи

Начать изучать бесплатно