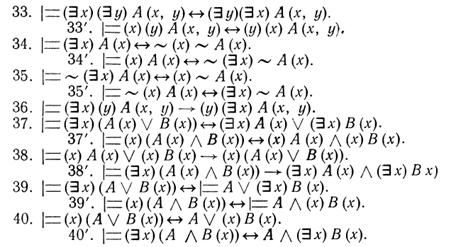Теорема 1. Пусть A(x) – формула, свободная для y. Тогда:
I. |=
II. |=
Следствие. Если |= , то |=![]() .
.
Теорема 2. Пусть x – какая-либо переменная, B – какая-либо формула, не содержащая свободных вхождений x, и A(x) – какая-либо формула. Тогда:
I. Если |=![]() , то |=
, то |=![]()
II. Если |= , то
Следствие: Если |= A(x), то |= .
Теорема 3. Пусть x и y – две различные переменные, A(x), B(x) и A(x,y) – любые формулы и A – любая формула, не содержащая свободных вхождений x. Тогда: