Как уже отмечалось, теорема F1; F2;…Fn|¾В равносильна доказательству |¾(F1&F2&…&Fn®B ). Если каждая Fi=и, то F1& F2&…&Fn )=и, а если (F1&F2&…&Fn®B)=и, то В=и.
Следовательно, при истинности всех посылок и истинности импликации (см. правило m.p.), заключение всегда будет истинным.
Используя правила эквивалентных преобразований алгебры высказываний, можно показать дедуктивный характер вывода заключения:
1) |¾(F1&F2&…&Fn®B);
2) |¾(ù(F1&F2&…&Fn )ÚB);
3) |¾(ùF1ÚùF2 Ú…ÚùFnÚB);
4) |¾(ùF1ÚùF2 Ú…ÚùFn-1Ú(Fn®B));
5) |¾(ùF1ÚùF2 Ú…Ú(Fn-1®(Fn®B)));
6) |¾(ùF1Ú(F2 ®…®(Fn-1®(Fn®B))…));
7) |¾(F1®(F2 ®…®(Fn-1®(Fn®B))…)
Так формируется система дедуктивного вывода от посылок до заключения.
Пример. Дано cуждение: “Всякое общественно опасное деяние (А) наказуемо (В). Преступление (С) есть общественно опасное деяние (А). Дача взятки (D) — преступление (C). Следовательно, дача взятки наказуема ?”[6].
![]() A®B;С®А; D®C
A®B;С®А; D®C
D®B.
1) F1=A®B посылка;
2) F2=С®А посылка;
3) F3=D®C посылка;
4) F4=C®B заключение по формулам F1 и F2 и
аксиоме А2 или правилу 11);
5) F5=D®B заключение по формулам F3 и F4 и аксиоме
А2 или правилу 11).
Следовательно, дача взятки (D) наказуема (B).
Пример: “Если Петров не трус (A), то он поступит в соответствие с собственными убеждениями (B). Если Петров честен (C), то он не трус (A). Если Петров не честен ù(C), то он не признает своей ошибки (D). Но Петров признает свои ошибки ù(D). Следовательно, он поступит согласно собственным убеждениям (B)?»[1]
![]() A®B; C®A; ùC®D; ùD
A®B; C®A; ùC®D; ùD
B.
1) F1=A®B посылка;
2) F2=C®A посылка;
3) F3=ùC®D посылка;
4) F4=ùD посылка;
5) F5=C®B заключение по формулам F1, F2 и аксиоме А2 или правилу 11);
6) F6=ùB®ùC заключению по формуле F5 и правилу 8);
7) F7=ùB®D заключение по формулам F3 и F6 и аксиоме А2 или правилу 11);
8) F8=B заключение по формулам F4, F7 и правилу m.t..
Так доказано, что Петров поступает согласно собственным убеждениям.
Пример: “Если команда А выигрывает в футболе то город А’ торжествует, а если выигрывает команда В, то торжествовать будет город В’. Выигрывают или А или В. Однако, если выигрывают А, то город В’ не торжествует, а если выигрывают В, то не будет торжествовать город А’. Следовательно, город В’ будет торжествовать тогда и только тогда, когда не будет торжествовать город А’”[1]
![]() (A®A’)&(B®B’); (AÚB); (A®ùB’)&(B®ùA’)
(A®A’)&(B®B’); (AÚB); (A®ùB’)&(B®ùA’)
(B’«ùA’).
1) F1=(A®A’)&(B®B’) — посылка;
2) F2=(A®A’) — заключение по формуле F1 и правилу удаления логической связки конъюнкции;
3) F3=(B®B’) — заключение по формуле F1 и правилу удаления логической связки конъюнкции;
4) F4=(A®ùB’)&(B®ùA’) — посылка;
5) F5=(A®ùB’) — заключение по формуле F4 и правилу удаления логической связки конъюнкции;
6) F6=(B®ùA’) — заключение по формуле F4 и правилу удаления логической связки конъюнкции;
7) F7=(B’®ùA) — заключение по формуле F5 и закону контрапозиции;
8) F8=(A’®ùB) — заключение по формуле F6 и закону контрапозиции;
9) F9=(AÚB) — посылка;
10) F10=ùA®B — заключение по формуле F9 и правилу эквивалентного преобразования;
11) F11=ùA®ùA’ — заключение по формулам F6, F10 и закону силлогизма;
12) F12= B’®ùA’ — заключение по формулам F7, F11 и закону силлогизма;
13) F13= ùA’®ùA — заключение по формуле F2 и закону контрапозиции;
14) F14=ùA’®B — заключение по формулам F10, F13 и закону силлогизма;
15) F15=ùA’®B’ — заключение по формулам F3, F14 и закону силлогизма;
16) F16= (B’®ùA’)(ùA’®B’)=(B’«ùA’) – заключение по формулам F12, F15 и правилу введения логической связки конъюнкции.
Так доказана истинность формулы (B’«ùA’).
Пример. «Если Петров говорит неправду (A), то он заблуждается (В) или сознательно вводит в заблуждение других (С). Петров говорит неправду и явно не заблуждается. Следовательно, он сознательно вводит в заблуждение других» [2]
![]() А®(ВÚС); A&ùB
А®(ВÚС); A&ùB
С.
1) F1=А®(ВÚС) — посылка;
2) F2=A&ùB — посылка;
3) F3=A — заключение по формуле F2 и правилу 2);
4) F4=ùB — заключение по формуле F2 и правилу 2);
5) F5=(ВÚС) — заключение по формулам F1, F3 и правилу m. p.;
6) F6=C — заключение по формулам F4, F5 и правилу 5).
Так доказано, что Петров сознательно вводит в заблуждение других.
![]() Пример: Доказать истинность заключения
Пример: Доказать истинность заключения
А;В;(А&С ® ù В)
ù C.
1) F1=A & C ® ù B — посылка;
2) F2=B — посылка;
3) F3=ù ( A & C ) — заключение по формулам F1, F2 и правилу m. t.;
4) F4= A — посылка;
5) F5=ù C — заключение по формула F3, F4 и правилу 2).
Процесс дедуктивного вывода удобно проследить на графе, вершинами которого являются формулы, а дугами – отношения между ними (см. рис.1).
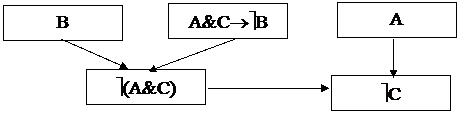 |
Рис.1. Граф вывода заключения
Пример. Доказать истинность заключения
(AÚB); (A®C); (B®D)
![]() (CÚD).
(CÚD).
1) F1=(A®C) посылка;
4) F2=(AÚB)®(CÚB) заключение по формуле F1 и правилу 9);
3) F3=(B®D) посылка;
4) F4=(CÚB)®(CÚD) заключение по формуле F3 и правилу 9);
5) F5=(AÚB)®(CÚD) заключение по формулам F2 и F4 и правилу 11);
6) F6=(AÚВ) посылка;
7) F7=(CÚD) заключение по формулам F5 и F6 и правилу m. p..
Так доказана истинность заключения (CÚD).
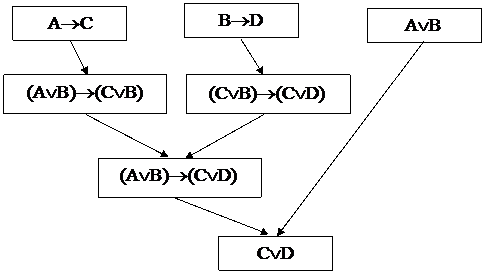 |
Рис. 2. Граф вывода заключения
Пример: Доказать истинность заключения
(A®B)&(C®D); ( D&B®E ); ù E
![]() ùC ÚùA.
ùC ÚùA.
1) F1=(D&B®E) посылка;
2) F2=ùE посылка;
3) F3=ù(D&B) заключение по формулам F1 и F2 и правилу m. t.;
4) F4=(А®В)&(С®D) посылка;
5) F5=(A®В) заключение по формуле F4 и правилу 2);
6) F6=(С®D) заключение по формуле F4 и правилу 2);
7) F7=(ùB®ùA) заключение по формуле F5 и правилу 8);
8) F8=(ùDÚùB) заключение по формуле F3 и закону де Моргана;
9) F9=(D®ùB) заключение по формуле 8) и правилу введения ипликации;
10) F10=(D®ù A) заключение по формулам F7 и F9 и правилу 11);
11) F11=(С®ù A) заключение по формулам F6 и F10 и правилу 11);
12) F12=(ùСÚù A) заключение по формуле FII и правилу введения дизъюнкции.
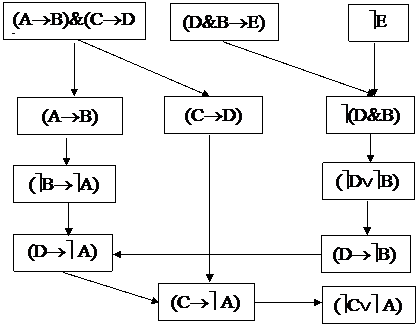 |
|||
|
|||
Пример: Доказать истинность заключения :
![]() ((A Ú B)® С); (С®(D Ú M )); (M®N); ((ù D)&(ù N))
((A Ú B)® С); (С®(D Ú M )); (M®N); ((ù D)&(ù N))
ù A.
1) F1=((ù D)&(ù N)) посылка;
2) F2=ùN заключение по формуле F1 и правилу 2);
3) F3=(M®N); посылка ;
4) F4=ùM заключение по формулам F2 и F3 и правилу m.t;
5) F5=ùD заключение по формуле F1 и правилу 2);
6) F6=(ùD)&(ùM) заключение по формулам F4 и F5 и правилу 1);
7) F7=ù(DÚМ) заключение по формуле F6 и закону де Моргана;
8) F8=(( AÚB)®C) посылка;
9) F9=(С® (DÚМ)) посылка;
10) F10=((AÚB)®(DÚM)) заключение по формулам F8 и F9 и правилу 11);
11) F11=ù(AÚB) заключение по формулам F7 и F10 и правилу m.t.;
12) F12=(ùА)&(ùB) заключение по формуле F11 и закону де Моргана;
13) F13=ùA заключение по формуле F12 и правилу 2).
Рис. 4. Граф вывода заключения
Эти примеры показывают, что правила вывода обеспечивают логическую последовательность в преобразовании формул, каждая из которых есть либо посылка, либо промежуточный результат, либо заключение.
