Под интерпретацией следует понимать систему, состоящую из непустого множества V, называемом универсумом, и однозначного отображения на двухэлементное множество {и; л}, которое каждому предикатному символу Pn (t1; t2;¼ tn ) ставит в соответствие n — местное отношение на множестве V, каждому функциональному символу f ni (t1; t2;¼ tn ) — n-местную операцию на множестве V, каждой предметной постоянной — элемент множества V.
При заданной интерпретации предметные переменные рассматриваются как переменные, пробегающие область универсума V, а символам логических и кванторных операций придается их обычный смысл.
Например, если универсум задан множеством целых чисел, то для $x $y $z (P2 (+(x, y); z)):= “существуют числа x, y, z, для которых z больше суммы чисел х и у», то при х=2, у=3, z=10 имеем двухместную операцию =5 и двухместное отношение между целым числом 10 и значением операции +(2,3)=5. Отображение P2(5;10) на двухэлементное множество дает значение “и”. При х=2, у=3, z=4 имеем +(2,3)=5 и P2 (5; 4)=л.
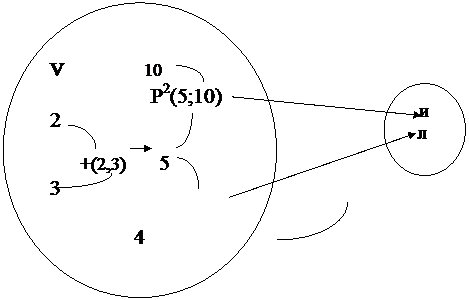
На рис. 10 приведена графическая интерпретация этой задачи.
 |
![]()
Рис.10 Интерпретация $x $y $z (P2 (+(x, y); z)) для x=2, y=3, z=10 или z=4.
Другими словами, интерпретация функциональных символов определяется по значениям функции на универсуме, заданном на множестве термов, входящих аргументами в эту функцию, а интерпретация предикатных символов по отображению на двухэлементное множество {и; л}.
Особо следует рассмотреть влияние свободных переменных на интерпретацию формул исчисления предикатов.
Формула, не содержащая свободных переменных, называется замкнутой и представляет собой высказывание об элементах, функциях и отношениях, которое принимает значение и или л. На рис. 10 рассмотрен случай замкнутой формулы.
Формула, содержащая свободные переменные, называется открытой и представляет собой отношений, заданное на множестве V,
Это отношение может быть истинным для одних значений из области интепретации и ложным для других.
При такой интерпретации выделяют три класса формул, тождественно истинные, тождественно ложные и выполнимые.
Тождественно истинные формулы (или тавтологии) -это особый класс формул исчисления предикатов, которые принимают значение “истины” для всех интерпретаций входящих в нее предметных постоянных, функциональных и предикатных символов; эти формулы играют роль законов и аксиом исчисления предикатов; любые подстановки и замещения в тождественно истинной формуле не изменяют ее значения.
Например,
для предиката P2(x, y):=”число x меньше числа y” формула «x$y(P2(x, y)):=”для любого целого числа x найдется число y, большее числа x” является тождественно истинной;
для любой F(x) формула $x(F(x))«ù»x(ùF(x)):=“формула ”существуют x, для которых F(x)=и”, эквивалентна формуле “не для всех x F(x)=л”” является тождественно истинной.
Тождественно ложные формулы (или противоречие)-это особый класс формул исчисления предикатов, которые принимают значение “ложь” для всех интерпретаций входящих в нее предметных постоянных, функциональных и предикатных символов; любые подстановки и замещения в тождественно ложной формуле не изменяют ее значения.
Например, для предиката P2(x, y):=”число x меньше числа y” формула $x»y(P2(x, y)):=”существует целое число x, которое меньше любого целого числа y” является тождественно ложной;
для любой F(x) формула $x(F(x))&»x(ùF(x)):=”“существует x, для которой F(x)=и”, и “для всех x F(x)=л ”” является тождественно ложной.
Выполнимые формулы— это особый класс формул исчисления предикатов, которые принимают значение “истина”в некоторой области, т.е. не для всех интерпретаций входящих в нее предметных постоянных, функциональных и предикатных символов.
Например, формула $x(F(x))®ù»x(F(x)) является истинной для одного элемента множества V и ложной для всех элементов этого множества, т.к.
$x(F(x))®ù»x(F(x)):=” если существует x, для которого F(x)=и, то не для всех х универсума F(x)=и” .
