В логике предикатов вывод определяется так же, как в исчислении высказываний. Все правила вывода логики высказываний включены в множество правил логики предикатов.
Пример: “Таможенные чиновники обыскивают каждого, кто въезжает в страну, кроме высокопоставленных лиц. Если некоторые люди способствуют провозу наркотиков, то на внутреннем рынке есть наркотик. Никто из высокопоставленных лиц не способствовает провозу наркотиков. Следовательно, некоторые из таможников способствуют провозу наркотиков?”
Пусть P1(x):=”x — таможенный чиновник”, P2(x,y):=”x обыскивает y”, P3(y):=”y въезжает в страну”, P4(y):=”y – высокопоставленное лицо”, P5(y):=”y способствует провозу наркотиков”.
«y(P3(y)&ùP4(y)®»x(P1(x)&P2(x,y)));
$y(P3(y)&P5(y));
![]() «y(P3(y)&P4(y)®ùP5(y));
«y(P3(y)&P4(y)®ùP5(y));
$x(P1(x)&P5(x)).
1) F1= $y(P3(y)&P5(y)) — посылка;
2) F2=P3(a)&P5(a) — заключение по формуле F1 и правилу удаления квантора существования;
3) F3= P3(a) — заключение по формуле F2 и правилу удаления логической связки конъюнкции;
4) F4= P5(a) — заключение по формуле F2 и правилу удаления логической связки конъюнкции;
5) F5=»y(P3(y)&P4(y)®ùP5(y)) посылка;
6) F6= P3(t)&P4(t)®ùP5(t) — заключение по формуле F5 и правилу удаления квантора общности;
7) F7=ùP3(t)ÚùP4(t)ÚùP5(t) — заключение по формуле F6 и ее эквивалентным преобразованиям;
8) F8=ùP4(a) — заключение по формуле F7 при t=a для ùP3(a)=л и ùP5(a)=л;
9) F9=»y(P3(y)&ùP4(y)®»x(P1(x)&P2(x,y))) — посылка;
10) F10=»y»x (P3(y)&ùP4(y)® (P1(x)&P2(x,y))) — заключение по формуле F9 и правилу приведения к ПНФ;
11) F11=P3(a)&ùP4(a)®P1(t)&P2(t,a) — заключение по формуле F10 и правилу удаления квантора общности;
12) F12= P3(a)&ùP4(a) — заключение по формулам F3 и F8 и правилу введения логической связки конъюнкции исчисления высказываний;
13) F13=(P1(t)&P2(t,a)) — заключение по формулам F11 и F12 и правилу modus ponens;
14) F14= P1(t) -заключение по формуле F13 и правилу удаления логической связки конъюнкции исчисления высказываний;
15) F15=P5(a)=P5(t) -заключение по формуле F4 и замене предметной постоянной термом;
16) F16= P1(t) &P5(t) -заключение по формулам F14 и А15 и правилу введения логической связки конъюнкция исчисления высказываний;
17) F17=$x(P1(x)&P5(x)) -заключение по формуле F16 и правилу введения квантора существования. Так доказана истинность формулы $x(P1(x)&P5(x)).
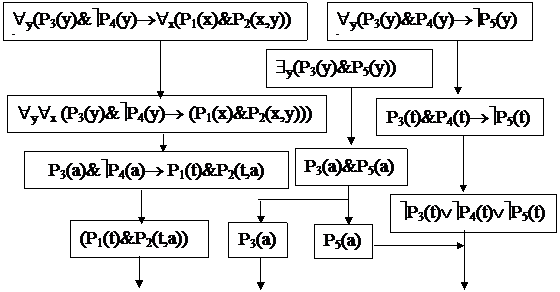
|
|
t=a
![]()
|
a=t ![]()
|
|
![]()
![]()
|
Рис. 11. Граф вывода заключения
Пример: Доказать истинность заключения
![]() «x( P1(x)®(ù P2(x))); «x(P3(x)®P1(x))
«x( P1(x)®(ù P2(x))); «x(P3(x)®P1(x))
«x(P3(x)®(ù P2(x))).
1) F1=»x( P1(x)®(ù P2(x))) — посылка;
2) F2=»x(P3 (x)®P1 (x)) -посылка;
3) F3=(P1 (t)®(ù P2 (t))) — заключение по формуле F1 и правилу 2) удаления квантора общности;
4) F4= P3 (t)® P1 (t) — заключение по формуле F2 и правилу 2) удаления квантора общности;
5) F5= (P3 (t)®(ù P2 (t))) — заключение по формулам F3, F4 и закону силогизма исчисления высказываний (см 1.2.3.2 правило 11);
6) F6=»x(P3(x)®(ùP2(x))) — заключение по формуле F5 и правилу 1 введения квантора общности.
Так доказана истинность формулы «x(P3(x)®(ùP2(x))).
На рис. 12 приведен граф, иллюстрирующий процесс дедуктивного вывода.
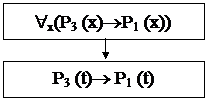 |
|||
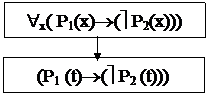 |
|||
![]()
![]()
|
![]()
|
Рис. 12. Граф вывода заключения
Пример: Доказать истинность заключения
![]() «x($y(P21.(x; y)&P2(y))®$y((P3(y)& P24.(x; y))); ù$x(P3(x))
«x($y(P21.(x; y)&P2(y))®$y((P3(y)& P24.(x; y))); ù$x(P3(x))
ù$x(P3(x))®»x»y(P21.(x; y)®(ùP2(y))).
1) F1=»x($y(P21.(x; y)&P2(y))®$y((P3(y)& P24.(x; y))) — посылка;
2) F2=ù $x(P3(x)) -посылка;
3) F3=»x(ùP3(x)) — заключение no формуле F2 и правилу 5) смены кванторов (закон де Моргана);
4) F4=ùP3 (t) — заключение по формуле F3 и правилу 2) удаления квантора общности;
5) F5=ùP3(t)ÚùP24.(x;t) — заключение по формуле F4 и правилу 4) исчисления высказываний;
6) F6=»y(ùP3(y)Ú(ùP24 (x; y))) — заключение по формуле F5 и правилу 1) введения квантора общности;
7) F7=ù$y(P3(y)&P24 (x; y)) — заключение по формуле F6 и правилу смены кванторов (закон де Моргана);
8) F8=$y(P21.(t; y)&P2(y)®$y(P3(y)&P24.(t; y)) — заключение по формуле F1 и правилу 2) удаления квантора общности;
9) F9=ù $y(P21.(t; y)&P2(y)) — заключение пo формулам F7 и F8при условии t=x и правилу modus tollens;
10) F10=»y(ù P21.(t; y)ÚùP2(y)) — заключение по формуле F9 и правилу смены кванторов (закон де Моргана);
11) F11=»y(P21. (t; y)®ù (P2 (y)) — заключение пo формуле F10 и эквивалентным преобразованиям алгебры предикатов;
12) F12=»x»y(P21. (x; y)®ù (P2 (y)) — заключение по формуле F11 и правилу 1) введения квантора общности;
13) ù$x(P3(x))®»x»y(P21.(x; y)®(ù P2(y))) – заключение по формулам F2 и F12 и правилу modus ponens. Что и требовалось доказать.
На рис. 13 приведен граф вывода этой задачи.

рис. 13 Граф вывода заключения
Пример. Доказать истинность заключения
![]() $x(P1(x)&»y(P2(y)®P24.(x; y))); «x(P1(x)®»y(P3(y)®ùP24.(x; y)))
$x(P1(x)&»y(P2(y)®P24.(x; y))); «x(P1(x)®»y(P3(y)®ùP24.(x; y)))
«x(P2(x)®ùP3(x)).
1) F1=$x(P1(x)&»y(P2(y)®P24.(x; y))) — посылка;
2) F2=»x(P1(x)®»y(P3(y)®ùP24 (x; y))) — посылка;
3) F3=P1(а)&»y(P2(y)®P24.(a; y))-заключение по формуле F1, правилу формирования ССФ;
4) F4=P1(a)- заключение по формуле F3 и правилу удаления конъюнкции исчисления высказываний
5) F5=»y(P2(y)® P24.(a; y)) — заключение пo формуле F3 и правилу удаления конъюнкции исчисления высказываний;
6) F6=P2(t)® P24.(a; t) — заключение по формуле F5 и правилу 2) удаления квантора общности;
7) F7=P1(t)®»y(P3(y)®ùP24 (t; y)) — заключение по формуле F2 и правилу 2) удаления квантора общности;
8) F8=»y(P3(y)®ù P24 (a; y)) — заключение по формулам F3 и F7 при t=a и правилу modus ponens;
9) F9=P3(t)®ùP24.(a; t) — заключение по формуле F8 и правилу 2) удаления квантора общности;
10) F10=P24.(a; t)®ùP3(t) — заключение по формуле F9 и закону контрапозиции (правило 8) исчисления высказываний);
11) F11=P2(t)®ùP3(t) — заключение по формулам F6 и F10 и закону силлогизма (правило 11) исчисления высказываний);
12) F12=»x( P2 (x)®ùP3(x)) — заключение по формуле F11 и правилу 1) введения квантора «x. Что требовалось доказать.
На рис. 14 приведен граф вывода этой задачи.
![]() x=a
x=a
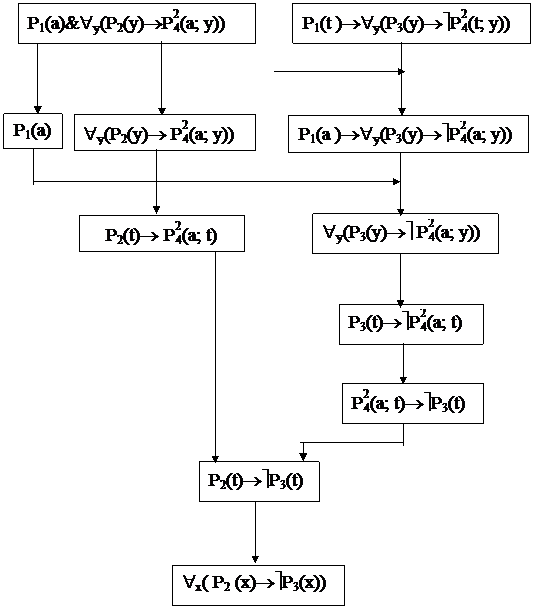 |
Рис. 14. Граф вывода заключения
