2.1.1 Декартово произведение
— мн-во всевозможных упорядоченных пар элементов из А и В.
Пример: 
2.1.2 Декартова степень произвольного множества.
Опр: — множество всевозможных упорядоченных наборов длины n , элементов множества А.
2.1.3 Определение булевой функции от n переменных.
Любое отображение 
— называется булевой функцией от n переменных, притом множество 
2.1.4 Примеры булевой функции.
1) 
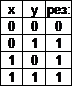
логическая сумма (дизъюнкция).
2) 
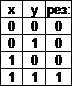
логическое умножение (конъюнкция).
3) 
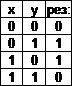сложение по модулю два.
4) 
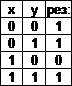логическое следствие (импликация).
5) 
отрицание.
2.1.5 Основные булевы тождества.
1) 
(ассоциативность)
2) (коммутативность)
3) 
(свойство нуля)
4) 
(закон поглощения для 1)
5) 
(ассоциативность)
6) 
(коммутативность)
7) (свойство нуля по умножению)
8) (свойство нейтральности 1 по умножению)
9) 
(дистрибутивность)
10) 
(дистрибутивность 2)
11) (закон поглощения)
12) 
( Законы
13) де Моргана)
14) 
(закон снятия двойного отрицания)
15) 
(tertium non datur – третьего не дано)
16) (ассоциативность)
17) 
18) 
19)
20)
21) 
(Свойства
22) 
идемпотентности)