Формула, истинностное значение которой есть T при любых возможных истинностных значениях, приписываемых ее простым компонентам, является тавтологией; говорят также, что такая формула общезначима (в исчислении высказываний).
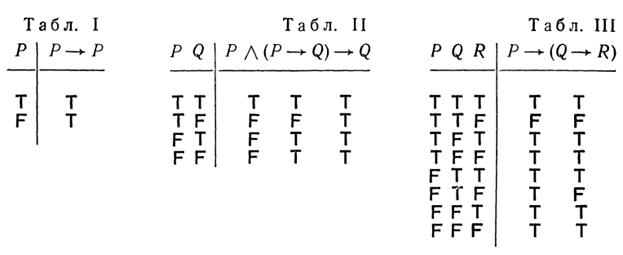
Дана формула А. Является ли она тавтологией или нет, можно определить, рассмотрев ее истинностную таблицу. Если простые компоненты, входящие в А, суть , то А представляет собой тавтологию тогда и только тогда, когда ее истинностное значение есть Т при каждом из приписанных распределений значений Т и F. Например, и являются тавтологиями, тогда как 
— не тавтология. Этот вывод основывается на рассмотрении помещенных ниже таблиц I, II и III.
Теорема. Пусть В есть некоторая формула, а — формула, получаемая из В подстановкой формулы А вместо простого компонента P везде, где он встречается в В. Тогда, если B – тавтология, то — также тавтология.
Пример: 
Подставим вместо P: