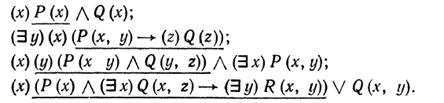Простая (или элементарная) формула есть выражение, получающееся из предикатного символа подстановкой в него вместо переменных, входящих в предикатный символ, каких-либо переменных. Например, из предикатного символа 
получаются простые формулы 
и 
. Мы расширим множество простых формул, присоединив к нему все те выражения, какие можно образовать, применяя повторно и всевозможными способами сентенциональные связки и кванторы. Точнее, мы расширим множество простых формул до такого наименьшего множества, которое удовлетворяет следующим условиям: если А и В – элементы данного множества, то элементами его будут и 
. Кроме того, если А – элемент данного множества, а x – переменная, то 
и 
— тоже элементы этого множества. Элементы такого расширенного множества называются формулами. Те из них, которые не являются простыми, называются составными формулами.
В состав формулировки исчисления предикатов необходимо ввести определения, позволяющие отличать обстоятельства, в которых переменная должна играть роль переменной, от обстоятельств, в которых она играет роль неизвестного в интуитивном смысле. В качестве предварительного шага определим область действия квантора, входящего в некоторую формулу, к которой он относится. Возможная двусмысленность устраняется применением скобок. Приведем несколько примеров, иллюстрирующих область действия квантора «(x)». Область действия показана подчеркиванием:
